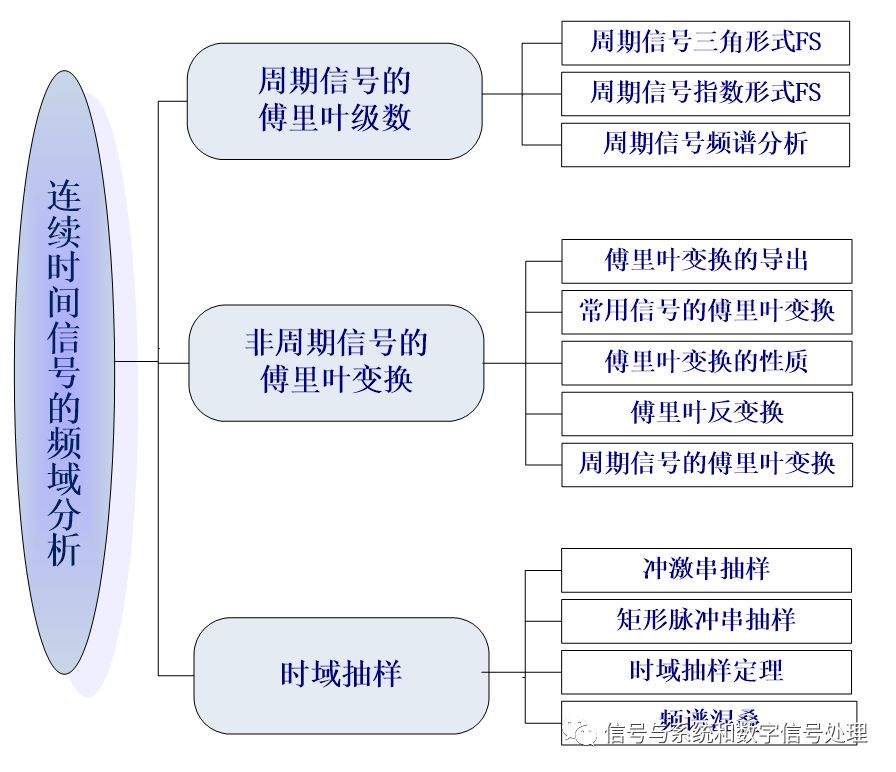
Frequency-domain analysis of continuous-time signals is one of the most important aspects of the course and is also the focus of the exam. It includes three aspects: the Fourier series of periodic signals, the Fourier transform of non-periodic signals, and time-domain sampling. The specific content is shown in the figure below.
This article includes the first two parts: the Fourier series of the periodic signal, the Fourier transform of the aperiodic signal.
Say at the front:
With the help of the Fourier series, we can step into the world of frequency domain analysis. Unfortunately, the somewhat cumbersome representation and derivation process of the Fourier series made many people daunting and hampered the self-confidence of learning this course. The more they learned, the more they did not want to learn, and even gave up. Therefore, I urge everyone to practice a fiery eye when studying or reviewing this part of the Fourier series. Through tedious mathematic deductions and calculations, we must see the hidden physical meaning behind it. Especially to the Fourier transformation part, there will be many magical and wonderful conclusions, like sparkling jewels, to attract everyone to learn signals and systems.
First, the Fourier series of periodic signals (CTFS)
"Fourier series of periodic signals" is a stepping stone to open the door of "Frequency domain analysis", and it is a bridge connecting time domain and frequency domain.
The main contents include:
1. Triangular FS and Exponential FS
The following figure shows the triangular and exponential FS expansion and the formula for solving the coefficients.


The fundamental difference between triangular FS and exponential FS lies in the following formula:
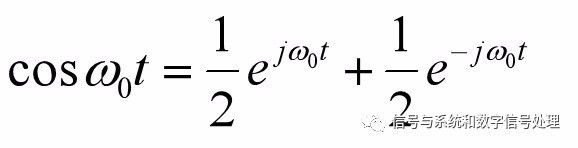
The exponential form of the Fourier series has a negative frequency term, which is just a matter of expressing the form. It does not mean that there is really a component that oscillates at a negative frequency. The negative frequency term and the corresponding positive frequency term together represent an oscillating component.
Need to master:
First, the characteristics of two types of orthogonal signal sets;
Second, the expansion of the two forms of FS expressions and coefficient solutions (key points).
According to the different time domain expressions of periodic signals, the solution method is divided into two types:
First, when the signal is directly written in the form of the sum of several sine and cosine functions, it is directly compared with the standard form of the FS expansion to obtain the FS coefficient. For example:


Second, the general periodic signal, you need to use the formula to solve the integral calculation. For example, the FS of a periodic rectangular pulse signal. This example is generally available in textbooks and is not repeated here.
2. Frequency spectrum analysis of periodic signals
Here is the concept of "spectrum" given for the first time in this course. Using the spectrum to describe the signal, we must accept and master this new form of description signal, clarify the time-frequency correspondence, and lay the foundation for the follow-up courses.
First, master the concept of spectrum. Derived "amplitude spectrum", "phase spectrum", "unilateral spectrum", "bilateral spectrum" and other terms.
From the point of view of the question, we summarize it, as shown below.

Second, the characteristics of the periodic signal spectrum: discreteness, harmonics, convergence
Third, the relationship between time domain parameters and spectral characteristics of periodic signals
Taking a periodic rectangular pulse signal as an example to analyze. As shown below.
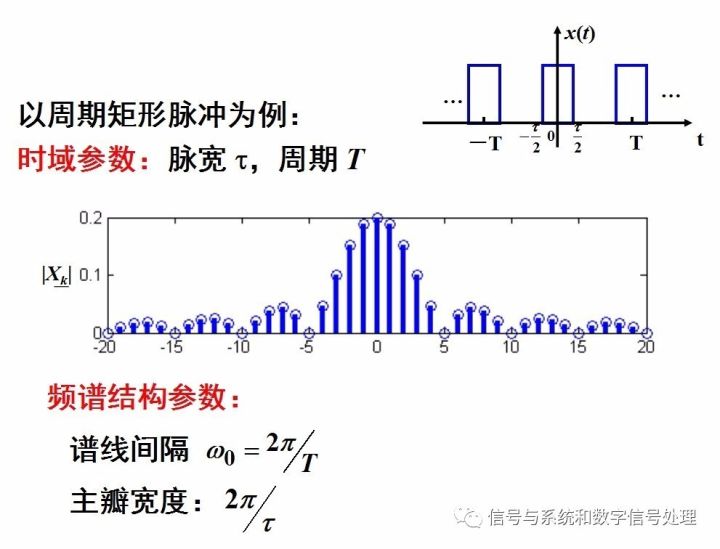
Get the following conclusions:

Fourth, the relationship between the symmetry characteristics of the time domain waveform and the Fourier coefficients
If the time domain waveform has some kind of symmetry, its Fourier series will show some special features, as shown in the figure below.
This particularity, when used to solve Fourier series coefficients for some periodic signals, can be simplified if used properly.

Second, the non-periodic signal Fourier transform (CTFT)
The Fourier transform is the focus of the focus. Including the following aspects:
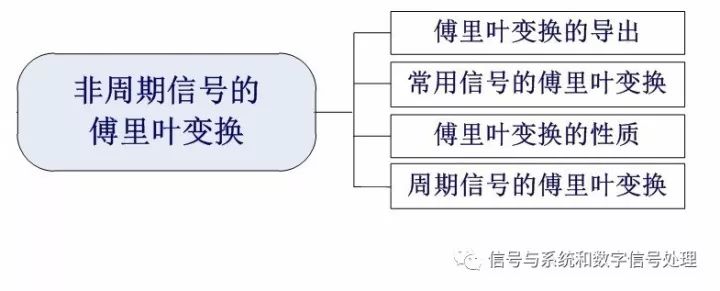
1, the export of the Fourier transform
As shown below.
The period T → infinity, spectral line interval → infinitesimal, discrete spectrum → continuous spectrum, but at the same time, the spectral line amplitude → infinitesimal, at this time, the spectrum is not suitable with FS. We have noticed that while the spectral lines tend to be infinitely small, the relative sizes are still different.
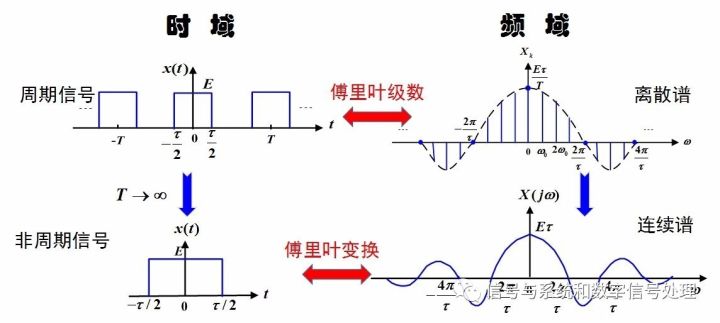
With the concept of physical "density", mass/volume = density. The Fourier transform X(jw) of the aperiodic signal is derived. Its meaning is the spectral value in the unit band and is called the “spectral density functionâ€.
2, the Fourier transform of commonly used signals
Impulse signal, step signal, sign function, DC signal, sine signal, cosine signal, unilateral exponential decay signal, bilateral exponential decay signal, gate function (rectangular pulse signal), bell pulse signal (Gaussian pulse), raised cosine Pulse signal, sinc function and so on. And their various derivatives and derivatives.
These common signals include ordinary signals and singular signals; those satisfying absolute integrable conditions do not satisfy absolute integrable conditions. Their Fourier transform solution is divided into three cases:
The first one is to directly use the definition formula to solve; the second is to use existing transformation pairs and properties to solve; the third is to special methods (such as the step signal u(t), symbol function, etc.).
Some to remember, some (such as bilateral exponential signals, bell-shaped pulses, raised cosine pulses, etc.) can be derived.

3, the nature of the Fourier transform
Using the Fourier Transform tool, we can derive its frequency domain description (X(jw)) from the time domain description of the signal (function x(t) with time t as an independent variable), and vice versa. The nature of the Fourier transform is to study the correspondence between these two domains, the time domain and the frequency domain. What is the correspondence? We can use two sentences to summarize. In the first sentence, what characteristics of some features in one domain correspond to another? In the second sentence, what happens to an operation in one domain in another domain? Specifically, what features and which operations? For example, parity symmetry, expansion and contraction operations, translation, integration/differentiation and so on.
In any textbook, there is a list of Fourier transform properties, which is not exhaustive. Focus on the following:
Scaling characteristics
The Fourier transform of the rectangular pulse signal can exhibit the expansion and contraction properties particularly intuitively.

The pulse width of the rectangular pulse increases, and in the time domain, the non-zero time range increases; in the frequency domain, the frequency spectrum is more concentrated near the frequency origin. That is, "time domain expansion, spectral compression," and vice versa.
Scaling and contraction characteristics, theoretically proved the inverse relationship between time domain and frequency domain, and also proved that the time-bandwidth product of the signal is equal to the constant. In communications, if you want to compress the duration of the signal, the bandwidth of the signal must be widened. To compress the effective frequency band of a signal, the duration of the signal has to be increased.
In general, the time domain is limited and the spectrum is infinite, and vice versa. There are no signals that have limited time and frequency domains.
Time-shift frequency shift characteristics
The time domain shift corresponds to the frequency domain, and the amplitude-frequency characteristic does not change, and the phase spectrum generates additional linear changes (+wt0). Therefore, the shape of the waveform does not change, because the relative magnitude relationship of the respective frequency components does not change (the corresponding amplitude spectrum does not change), and the relative positional relationship on the time axis does not change (a wt0 is added to the corresponding phase, and is linearly related to w).
Frequency shift, spectrum shifting is a widely used technology in communication systems, such as modulation, demodulation, frequency conversion, etc., are all completed on the basis of frequency shift, and frequency shift characteristics are its theoretical basis.
Using the frequency shift feature, we can derive the Fourier transform of the imaginary exponential signal and the sine cosine signal. All three signals are not satisfying the conditions of absolute integrability, and there are impulse functions in the Fourier transform.

Differential characteristics
The time-domain differential characteristics and frequency-domain differential characteristics can be used to solve pairs of transformations that cannot be or cannot be easily solved using formulae, such as impulse couple functions, tu(t), and so on.
Differential characteristics are important in the frequency domain analysis of the system. Because it is the differential equation that describes the continuous-time system, we can think of that the Fourier transform method will be very useful in the solution of differential equations (ie, system response solving) and system analysis.
Integral characteristics
Integral characteristics are also mainly used to solve Fourier transforms of some more complex signals. However, when applying it, it should be noted that the integral characteristic cannot be used as the inverse of the differential characteristic, and the DC component of the integral characteristic must be noted. Otherwise, an error will occur.
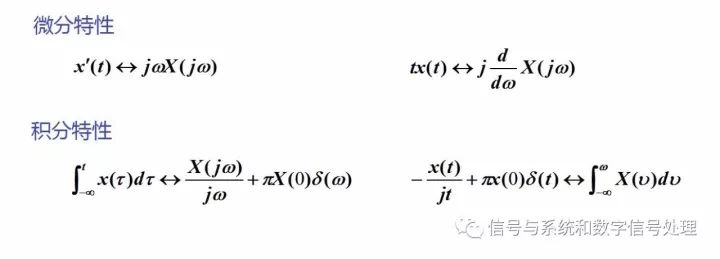
Convolution characteristics
Including the time domain convolution property and the frequency domain convolution property, a domain multiplication, another domain convolution, this is a very basic, very important relation.
A method for calculating the Fourier transform is provided, and at the same time, it is the basis of the frequency domain analysis of the system.
Reciprocal symmetry
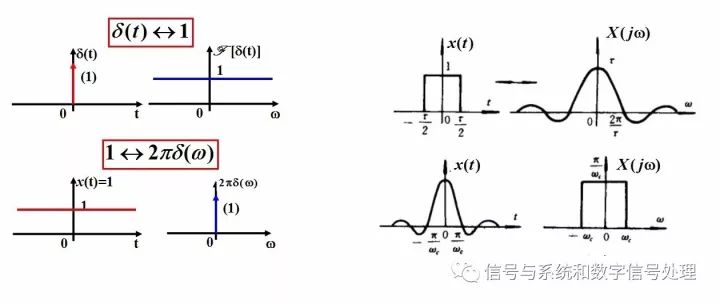
In the end, let's talk about this magical and beautiful nature.
If a signal has a red characteristic in the time domain, it has a blue characteristic in the frequency domain, and another signal has this blue characteristic in the time domain, then it is in the frequency domain. It will behave in a way that resembles the kind of red that was just now.
Many transformation pairs reflect this. For example, the impulse signal in the time domain has a spectrum of 1; while the direct current 1 in the time domain corresponds to a spectrum of 2Ï€ times the impulse function. For another example, the rectangular pulse in the time domain has a sinc function in the frequency spectrum, and the sinc signal in the time domain has a rectangular function in the frequency spectrum.
This is also reflected in the nature of many Fourier transforms, such as time-shift characteristics and frequency shift characteristics, time-domain differentiation and frequency-domain differentiation, and so on.

Finally, mention the inverse Fourier transform solution method, there are the following three:
Solving using the definition of the inverse Fourier transform
Solving the nature of FT
Pay special attention to the application of reciprocal symmetry.
Partial fractional expansion
The partial fractional expansion method is not only one of the solutions to the inverse Fourier transform, but also the inverse transform method for the backward Laplace transform and z transform.
4, the Fourier transform of the periodic signal
The periodic signal, which does not satisfy absolute integrability, does not converge if it is brought into the Fourier transform formula. Does that mean that the Fourier transform of the periodic signal does not exist? no. When we talked about the properties of the Fourier transform, we have solved the Fourier transform pairs of the sine and cosine signals and found that they have an impulse function in the Fourier transform. Therefore, by introducing an impulse function, we do not satisfy the absolute The integrable conditional periodic signal can also be represented by a Fourier transform. In this way, the Fourier transform unifies the Fourier series.
What is the relationship between the Fourier series and the Fourier transform? It is easy to understand the relationship between the two with the following diagram.
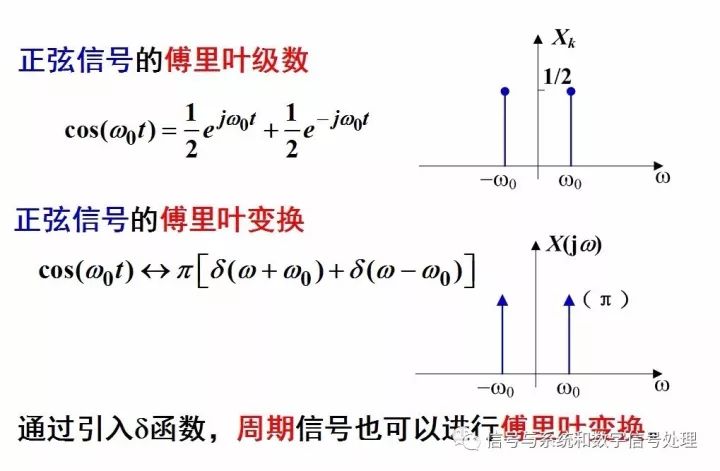
The Fourier transform of a periodic signal is a series of linear combinations of intensities of 2Ï€Xk that occur at the harmonic frequency kw0 and are still discrete spectra.
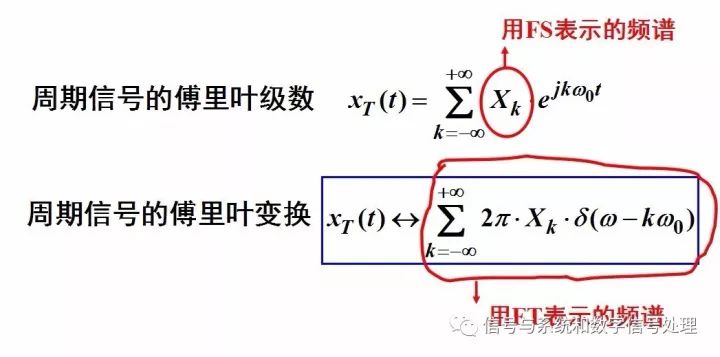
A very important, very interesting, very beautiful pair of transformations can be derived, as shown below
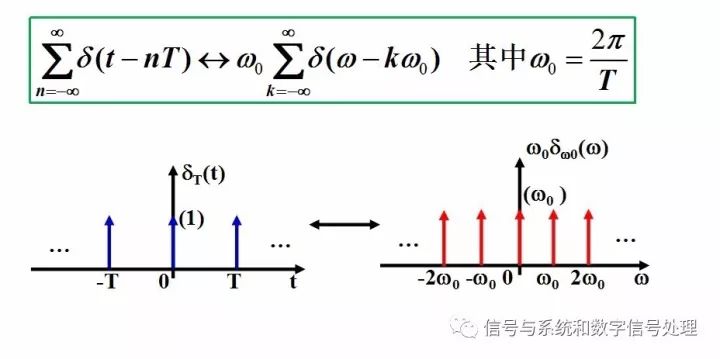
The pair of transformations shown above will play an important role in the “time domain sampling†section.
Protected Silver Mirrors with average reflection >96% for 400 nm-IR. These mirrors feature higher reflectance than aluminium throughout the visible and near-infrared spectral region.Enhanced silver mirrors designed for applications with femtosecond lasers. Reflectivity R>98.5% at 600 - 1100 nm wavelength range and R>99% at 700-900 nm.
Ag Coating Mirrors,Silver Coating Mirrors,Protective Silver Mirror,Metallic Mirror
Zoolied Inc. , https://www.zoolied.com